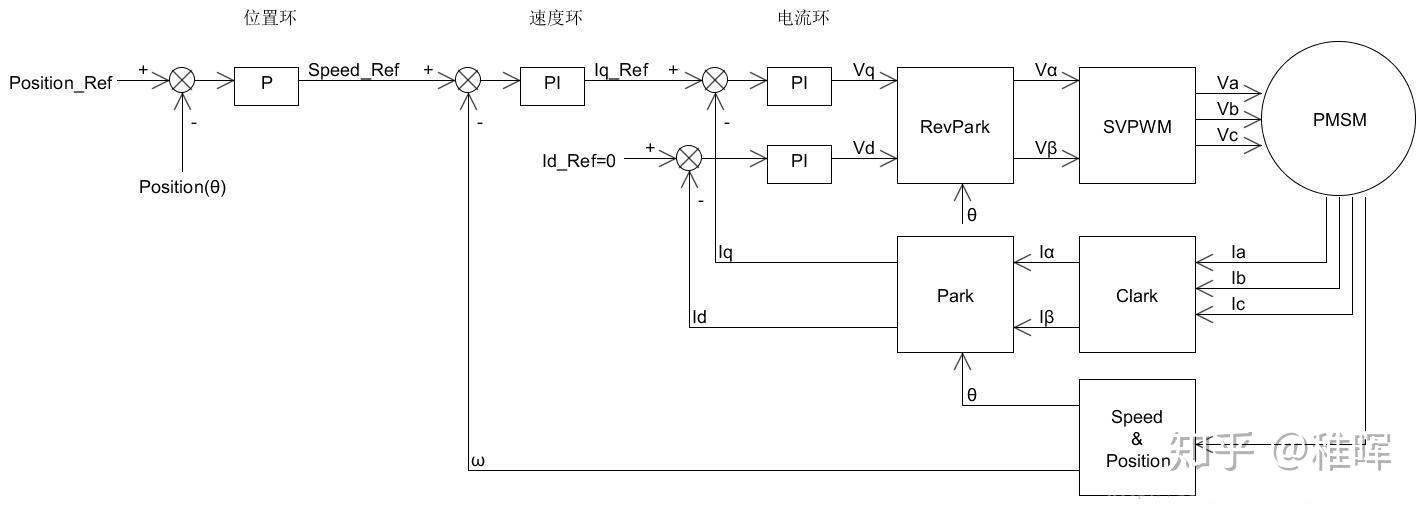
一、总览
我们按照让电机开环转起来->电流环闭环->速度、角度环闭环这个顺序进行学习
也就是帕克逆变换->SVPWM（到这里已经可以让电机开环转动）->克拉克变换->帕克变换（到这里完成电机中最重要的电流闭环）中间会补充一些电角度的细节和PID的知识
强烈建议先阅读一遍稚晖君关于FOC算法的讲解，文章言辞通俗，对算法知识点到即止。非常适合新人入门看，老手看也是常看常新
(2 条消息) 【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术 - 知乎
二、帕克变换及其逆变换（将Uq、Ud加上编码器的角度值转换成两项正弦波）
1.帕克变换是什么
怎么才能让克拉克变换之后的两项正弦波变成不动的两个量呢？
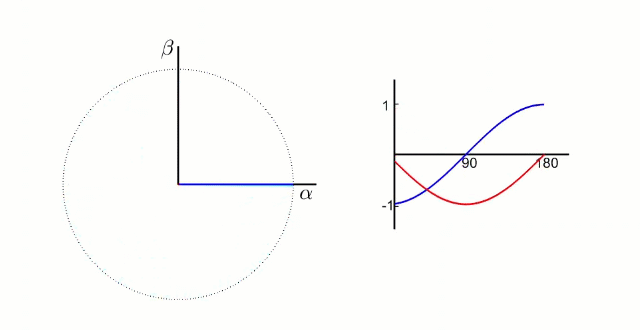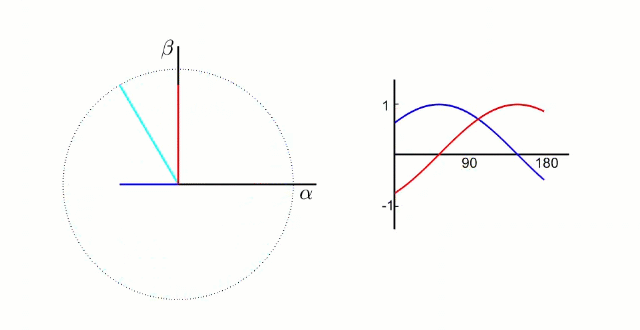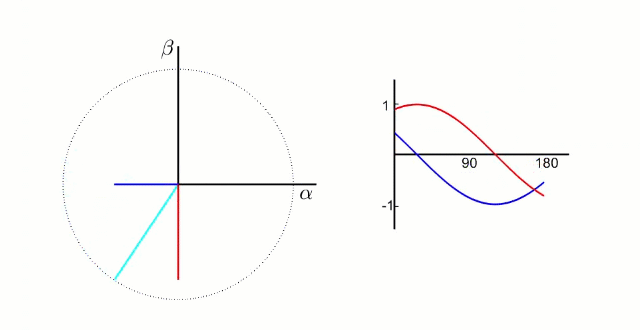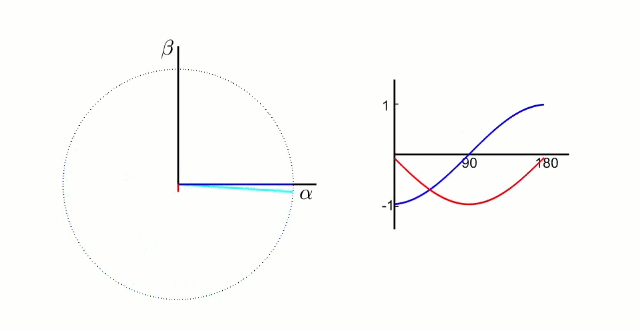我们知道这两个正弦波是由于中间的电压合成矢量旋转过程中分解到两个坐标轴上形成的，我们可以想到如果让参考系和中间的电压合成矢量一起旋转不就行了吗，在参考系看来这个电压矢量不就是不动的吗？对的，这就是帕克变换的内容了，也被叫做旋转矩阵，他不仅可以用在FOC中用来对三项电压进行”降维“，还可以运用在robomaster的小陀螺上。
2.帕克变换形式
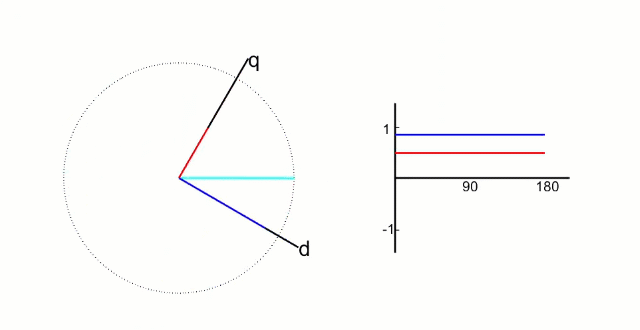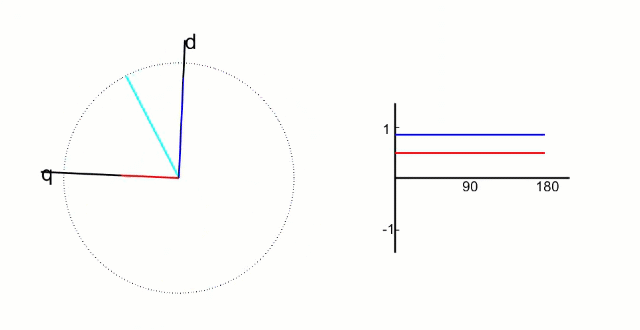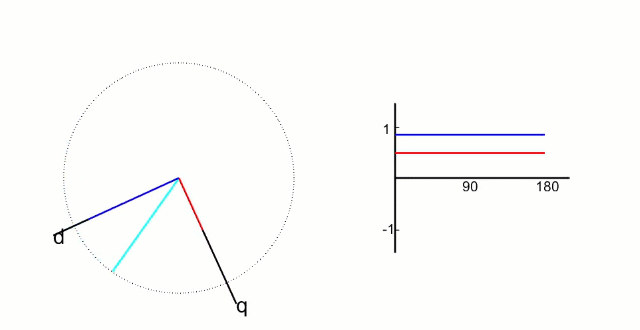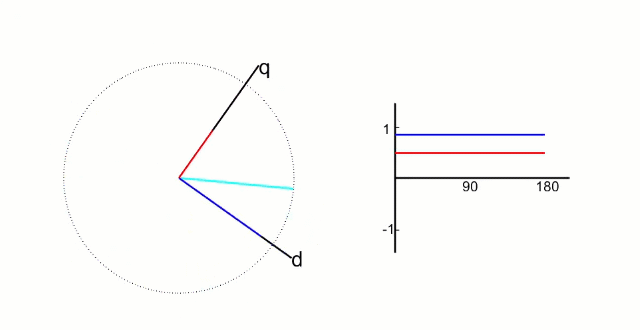
我们已经知道帕克变换就是将两项正弦波配合上帕克变换参考系的同步旋转，使得两项正弦波在帕克变换参考系上分解为定值
我们引入一个参数theta表示帕克参考系相对克拉克参考系的旋转角度，
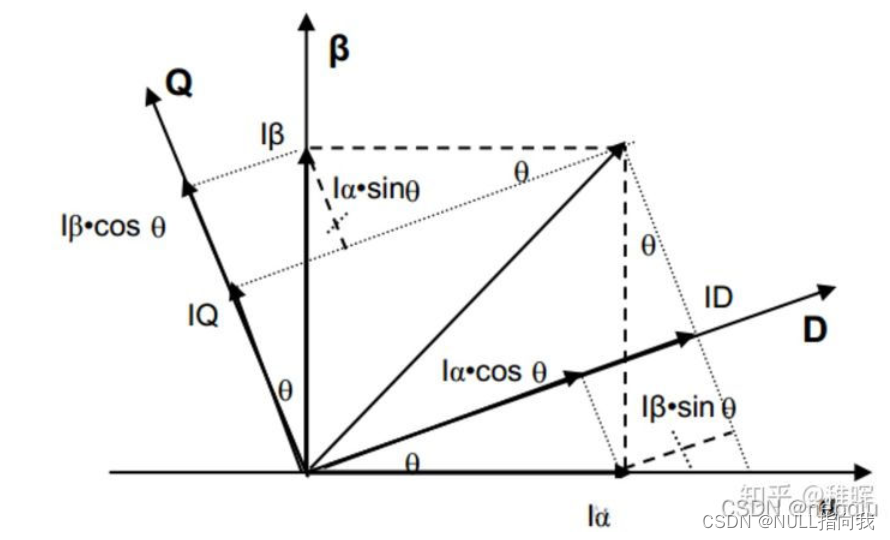
有了theta参数，我们就可以将克拉克坐标分解到帕克坐标系中了。
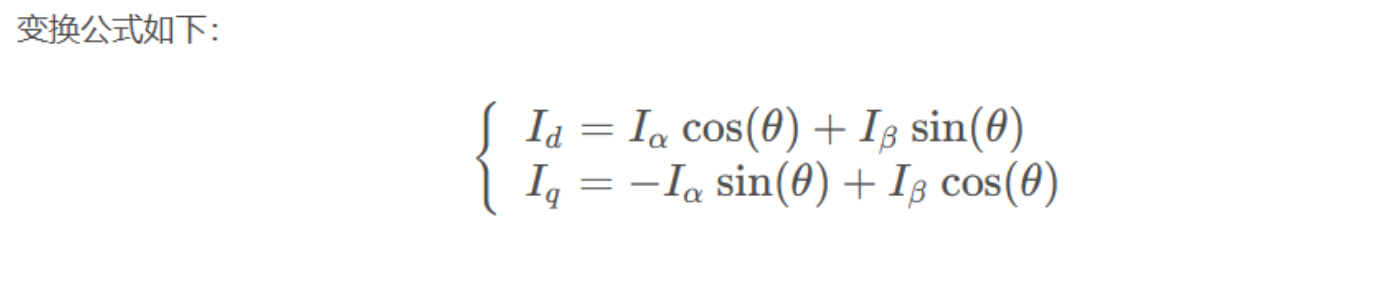
没错，帕克变换就是上面这两个等式。下面给出帕克变换的代码
void Park_Transform(const float Ialpha, const float Ibeta, float theta, float *Id, float *Iq) {
const float cos_val = arm_cos_f32(theta);
const float sin_val = arm_sin_f32(theta);
*Iq = cos_val*Ibeta - sin_val*Ialpha;
*Id = cos_val*Ialpha + sin_val*Ibeta;
}帕克逆变换也大差不差，现在已经抛弃了常规算法，改用直接调用arm库了，强烈建议使用arm库，arm库对很多算法都有支持，比如这里的帕克变换，还有克拉克变换，甚至还有PID。这些函数你都可以在编辑器上打出”arm_“通过编译器提示进行一览。
/**
* @brief 反Park变换 (dq -> αβ)
* @param Ud: d轴电压分量
* @param Uq: q轴电压分量
* @param Ubeta: 输出参数，β轴电压分量
* @param cos_theta: 角度余弦值
* @param sin_theta: 正弦值
* @param Ualpha: 输出参数，α轴电压分量
*/
void Inverse_Park_Transform(float Ud, float Uq , float *Ualpha, float *Ubeta,float sin_theta,float cos_theta)
{
arm_inv_park_f32( Ud, Uq, Ualpha, Ubeta,sin_theta,cos_theta);
//
//常规方法
// // 高效角度归一化 (0 ~ 2π)
// theta = fmodf(theta, 2.0f * PI);
// if (theta < 0) theta += 2.0f * PI;
//
// float sin_val = arm_sin_f32(theta);
// float cos_val = arm_cos_f32(theta);
//
// *Ualpha = Ud * cos_val - Uq * sin_val;
// *Ubeta = Ud * sin_val + Uq * cos_val;
}推荐资料：
【手把手教写FOC算法】4_帕克变换(新手入门推荐，讲的很通俗)
三、SVPWM（FOC算法核心）
1.SVPWM是干什么的
如果把SVPWM看也做黑盒子，那么他输入由帕克逆变换得到的Uα和Uβ，输出是当前三相需要的高电平时间或者说是CCR值。他可以利用六个基本的电压矢量（分立的）通过七段式切换 合成连续的、任意方向的矢量。
2. SVPWM如何工作？
首先我们需要先让电机绕组产生360度全方位的磁矢量，产生了磁矢量之后电机的转子（也可以看做一块磁铁）会被产生的磁矢量所吸引到对应的方向，这样就达到了我们控制电机转动的目的
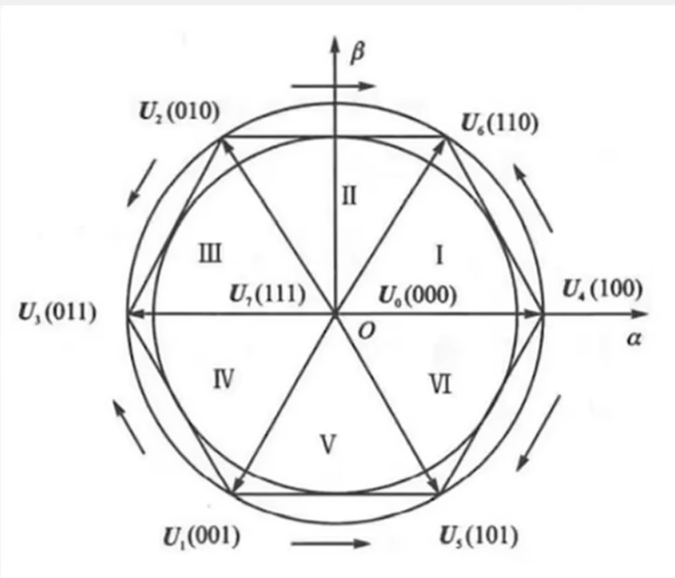
我们通过对A、B、C三相线的一进两出，两进一出，得出了右边的六个全部的基本磁矢量（电压矢量），有了这六个基本电压矢量之后我们就可以合成其中的任何方向的电压矢量，比如我要产生一个U4（100）和U6（110）之间的一个电压矢量，就可以通过U4和U6交替切换根据伏秒平衡原理产生其中任何方向的电压矢量
那么这六个基本电压矢量合成的合成的就是以基本电压为半径的圆吗？不是的。
我们可以使用一个简单的实验对其进行验证
假如我们想要合成U4和U6正中的一个电压矢量，那么我们很简单可以知道此时U6和U4在单个切换周期内是各占一半的。因此我们可以得到图中公式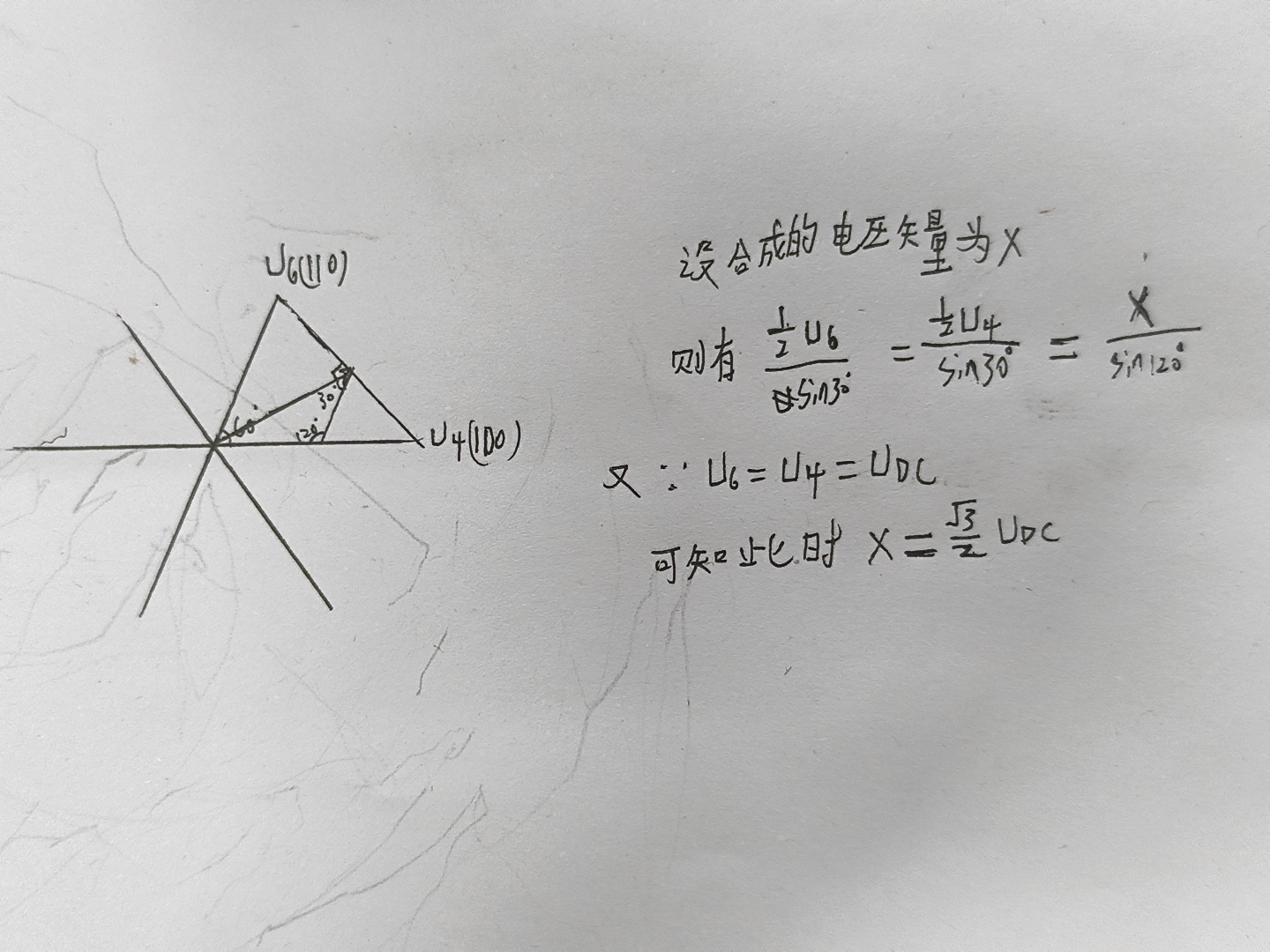
得到的结果是二分之根号三，刚刚好是直线连接U6和U4的线到中性点的距离！同理我们也可以知道其他情况下合成出来的电压矢量的大小就是基本电压矢量围成的六边形。而我们都知道中性点到六边形的距离在U6到U4(其他扇区内也是同理，这里只是举个例子)是先减小后增大的，这样，我们SVPWM标志性的马鞍波就出来了。*问题4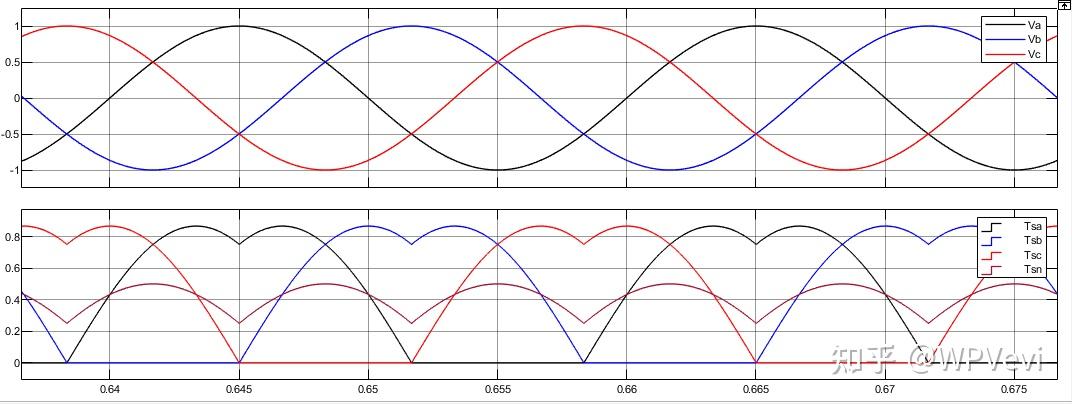
我们再根据上面的基础上合成一个与U4角度为θ的电压矢量，还是和刚才一样的用正弦定理，最后得出相邻两项基本电压矢量的切换时间：
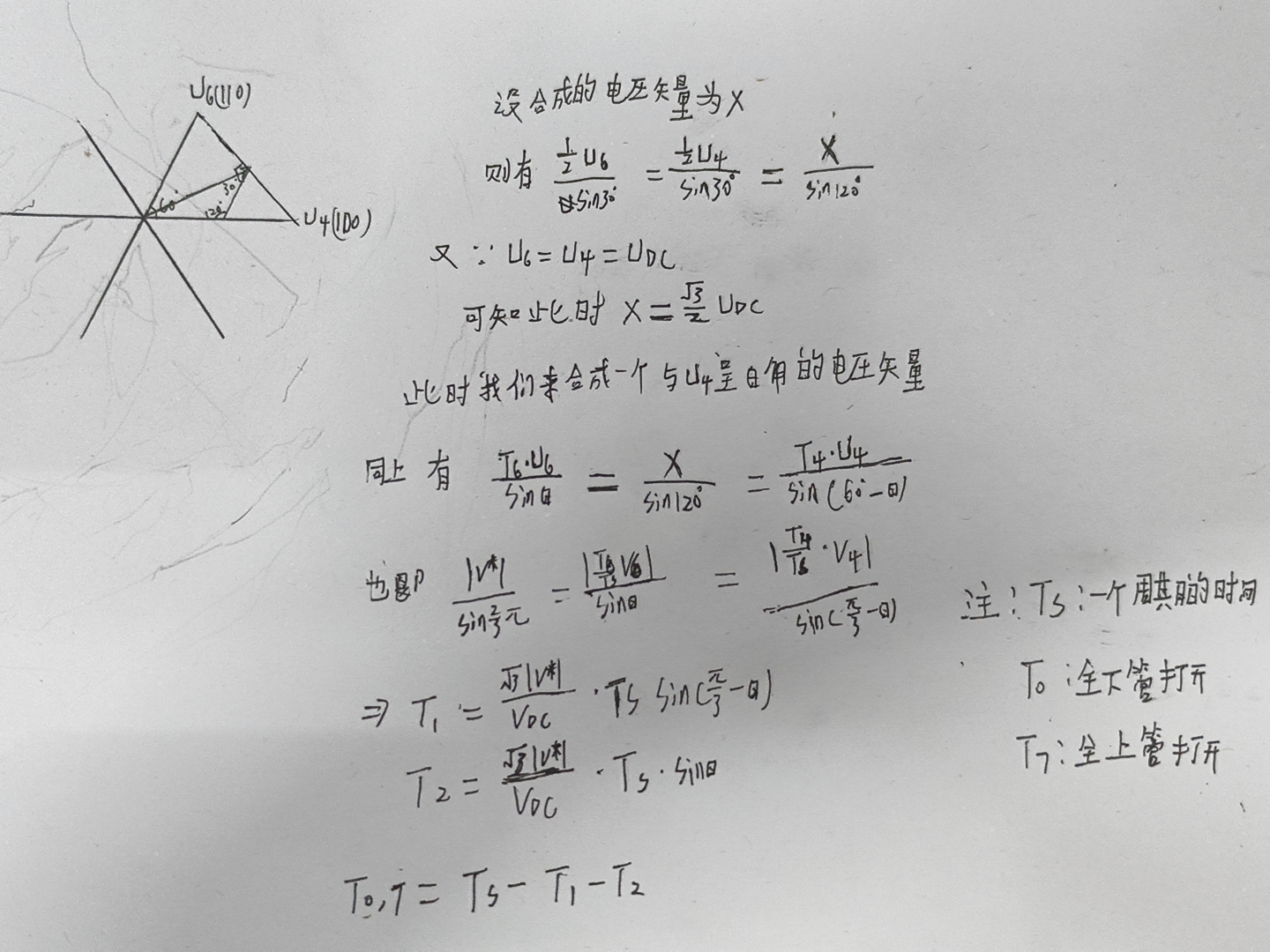
T1=(sqrt(3)*Vx*Ts*sin(PI/3-theta))/Udc;
T2=(sqrt(3)*Vx*Ts*sin(theta))/Udc;
那么我们接下来就要把这个T1和T2转换成CRC的比较值，这样就可以通过PWM输出了
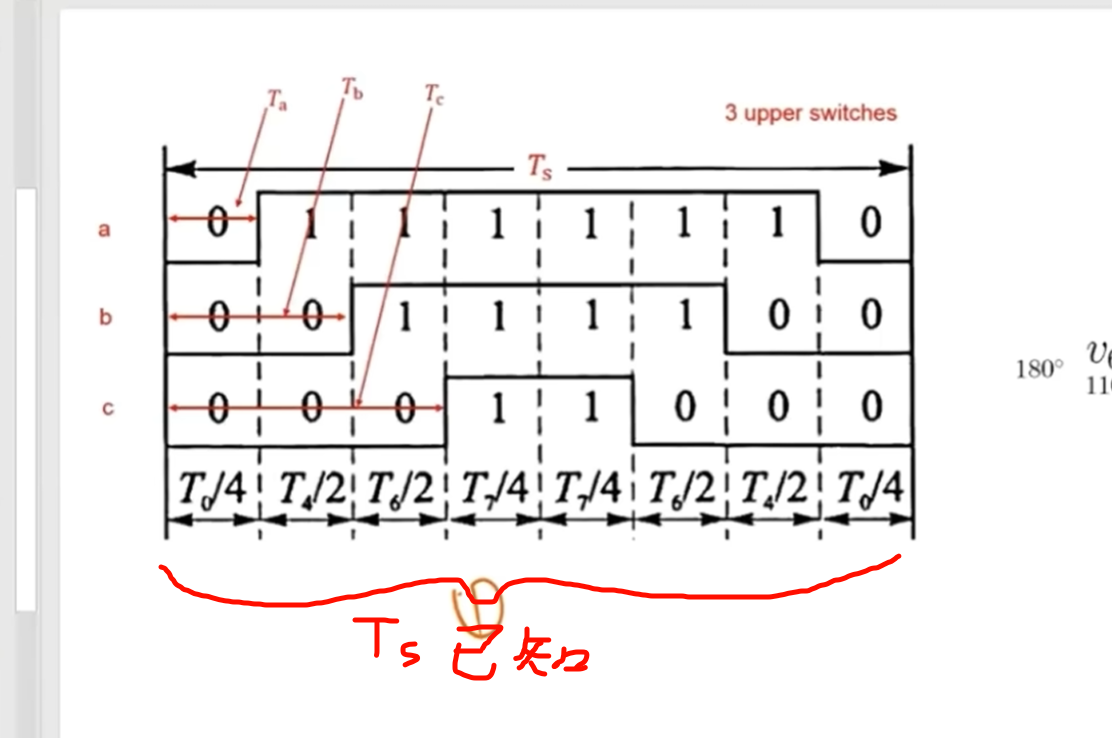
而我们已经知道Ts也就是占空比的最大值Ts了，T1和T2又已知，则T0、T7=Ts-T1+T2也很容易计算出来
结合图像可以知道
Tc_tempCCR=(T7、T0)/2;T0或T7的时间的四分之一，也是第一路的占空比,最底下的一路占空比
Tb_tempCCR=Tc_tempCCR+T1/2;//四分之一的T0加上T1的二分之一，中间一路占空比
Ta_tempCCR=Tb_tempCCR+T2/2;//四分之一的T0加上T1的二分之一加上T2的二分之一，最高一路占空比结束了吗？
我们可以知道不同的扇区的Ta、Tb、Tc对应的上下桥是不一样的，所以上面的Tc_tempCCR并不是指现实主板上的ABC三相占空比，我们需要将他们对应起来，比如我们在第一扇区，U4=100，U6=110。我们知道A相（两个基本向量的第一位数字）是打开时间是最多的，因为有两个打开，所以Ta_CCR=Ta_tempCCR。BC相也是一样的。我们再举个第四扇区的例子，在第五扇区，U1=001，U5=101。Ta_CCR=Tb_tempCCR，Tb_CCR=Tc_tempCCR，Tc_CCR=Ta_tempCCR。非常好理解。
然后我们PWM START就可以让电机转起来了！！！
我们还能不能优化一下上面的结构呢？
上面的需要知道theta，需要对Uα和Uβ进行反正切计算得到theta，计算T1、T2也需要进行昂贵的sin、cos计算，，这不是我们想要的。
我们想要避免正余弦、反正切计算，就需要抛弃掉theta，可是没有theta也能判断扇区吗？当然可以了。
我们在原有的扇区上基于αβ判断。根据αβ加上β=sqrt{3}α和β=-sqrt{3}α根据这样最简单的逻辑判断就可以
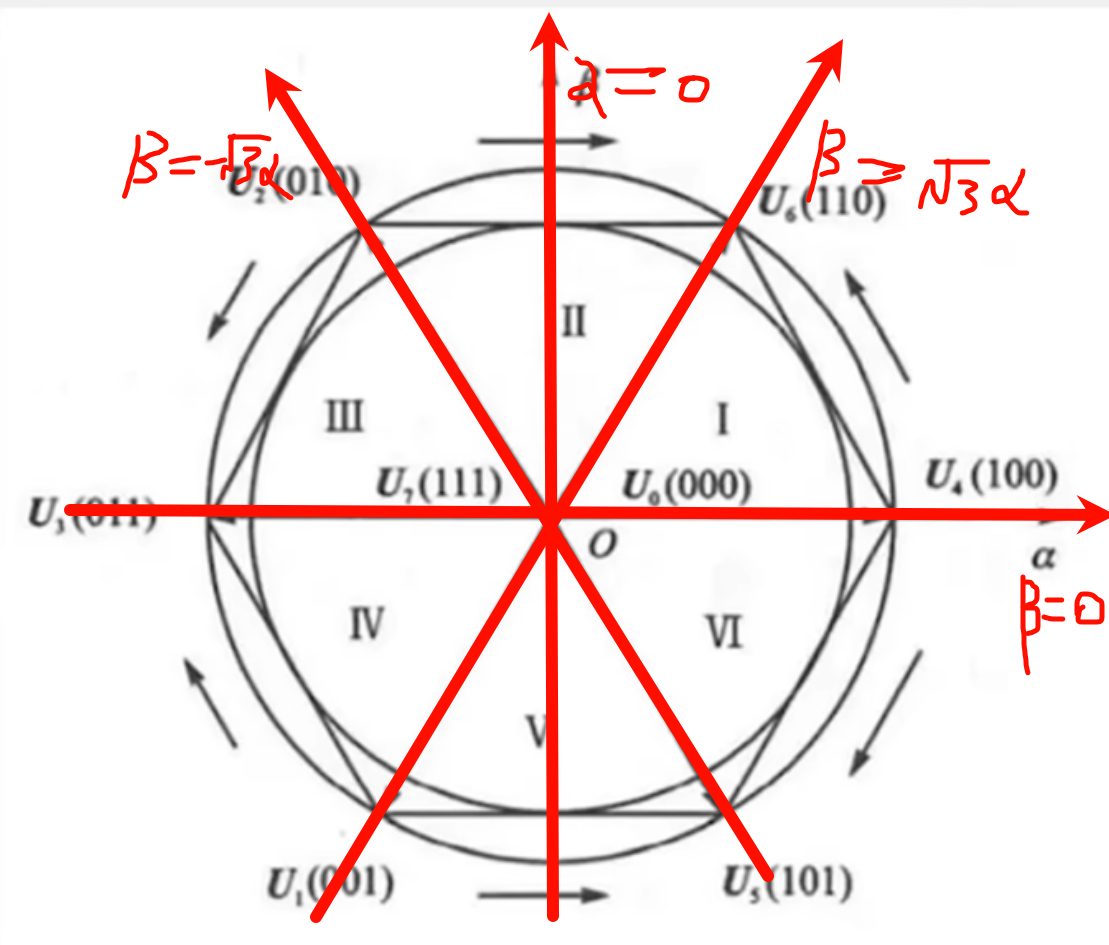
这里给出扇区判断函数
/**
* 判断扇区编号
* @param Ualpha α轴电压分量
* @param Ubeta β轴电压分量
* @param sector 输出参数，扇区编号 (1-6)
* @return 扇区编号 (1-6)
*/
uint8_t Get_Sector(float Ualpha, float Ubeta,uint8_t *sector) {
// 预计算三个比较值
float U1 = Ubeta;
float U2 = SQRT3*Ualpha-Ubeta ;
float U3 = - SQRT3*Ualpha -Ubeta;
bool A = false,B = false,C = false;
A=U1>0?true:false;
B=U2>0?true:false;
C=U3>0?true:false;
// 构建3位索引（ABC的符号组合）
uint8_t N = 4*C+2*B+A;
// 直接映射到扇区编号
static const uint8_t sector_map[6] = {2,6,1,4,3,5};
*sector = sector_map[N-1];
return sector_map[N-1];
}我们既然知道了扇区那么我们上面公式中计算T1，T2的正余弦函数的资源也可以节省下来了
可以通过中间变量去计算T1，T2（此处推导待补充）
// 2. 计算出中间变量X、Y、Z，在
const float32_t X=SQRT3*Ubeta*Ts/Udc;
const float32_t Y=Ts/Udc*(1.5f*Ualpha+SQRT3_2*Ubeta);
const float32_t Z=Ts/Udc*(-1.5f*Ualpha+SQRT3_2*Ubeta);
到这里知道扇区也知道T1，T2基础向量的大小了我们根据扇区给三相占空比赋值即可
此处附上SVPWM完整代码
/**
* SVPWM算法核心函数 - 计算三相PWM占空比,注意此处Ts、T1、T2、Ta、Tb、Tc都是对CCR的计算，并非时间
* @param Ualpha alpha轴电压分量 (V)
* @param Ubeta beta轴电压分量 (V)
* @param Udc 直流母线电压 (V)
* @param Ts ARR
* @param[out] TA A相PWM占空比 (0.0~1.0)
* @param[out] TB B相PWM占空比 (0.0~1.0)
* @param[out] TC C相PWM占空比 (0.0~1.0)
*/
void SVPWM_Calculate(const float32_t Ualpha, const float32_t Ubeta, const float32_t Udc, const float32_t Ts, float32_t *TA, float32_t *TB, float32_t *TC) {
// 1. 判断扇区
uint8_t sector =0;
Get_Sector(Ualpha, Ubeta,§or);
//printf("sector=%d\r\n", sector); // 输出扇区编号
// 2. 计算出中间变量X、Y、Z，在
const float32_t X=SQRT3*Ubeta*Ts/Udc;
const float32_t Y=Ts/Udc*(1.5f*Ualpha+SQRT3_2*Ubeta);
const float32_t Z=Ts/Udc*(-1.5f*Ualpha+SQRT3_2*Ubeta);
float32_t T1,T2;
switch(sector){
case 2:
T1=Z;T2=Y;
break;
case 6:
T1=Y;T2=-X;
break;
case 1:
T1=-Z;T2=X;
break;
case 4:
T1=-X;T2=Z;
break;
case 3:
T1=X;T2=-Y;
break;
case 5:
T1=-Y;T2=-Z;
break;
default:
T1=0;T2=0;
break;
}
// 3. 过调制处理
if(T1+T2 > Ts) {
const float32_t scale = Ts / (T1+T2); // 1次除法
T1 *= scale; // 1次乘法
T2 *= scale; // 1次乘法
}
const float32_t TA_temp=(Ts-(T1+T2))/4.0f;//T0或T7的时间的四分之一，也是第一路的占空比,最底下的一路占空比
const float32_t TB_temp=TA_temp+T1/2.0f;//四分之一的T0加上T1的二分之一，中间一路占空比
const float32_t TC_temp=TB_temp+T2/2.0f;//四分之一的T0加上T1的二分之一加上T2的二分之一，最高一路占空比
// 根据扇区映射到真正的上下管占空比
switch (sector) {
case 2:
*TA=TB_temp;
*TB=TA_temp;
*TC=TC_temp;
break;
case 6:
*TA=TA_temp;
*TB=TC_temp;
*TC=TB_temp;
break;
case 1:
*TA=TA_temp;
*TB=TB_temp;
*TC=TC_temp;
break;
case 4:
*TA=TC_temp;
*TB=TB_temp;
*TC=TA_temp;
break;
case 3:
*TA=TC_temp;
*TB=TA_temp;
*TC=TB_temp;
break;
case 5:
*TA=TB_temp;
*TB=TC_temp;
*TC=TA_temp;
break;
default:
*TA=0;
*TB=0;
*TC=0;
break;
}下图为SVPWM标志性的三相马鞍波形
问1：SVPWM判断扇区的算法不是多此一举吗？在实际的电机控制中，有感方案不是可以直接得到转子的位置从而得到theta，有theta转换成电角度不就知道扇区了吗，而无感方案中六步换相也不用判断扇区不是吗？
问2：SVPWM假如要合成一个U4（100）和U6（110）之间的一个电压矢量，不是只要调整第二项半桥的上下桥导通时间就可以吗？为什么还有000->100->110->111->110->100->000这样的七段式SVPWM调制法？这不是反而增加了半桥的开关损耗吗？
问3：为什么SVPWM矢量合成图是一个六边形，而不是圆形。或者说为什么经过SVPWM处理后是马鞍波，而不再是正弦波了
问4：马鞍波为什么会比正弦波好呢？既然马鞍波会比正弦波好，那我们一直研究三相正弦波是为什么呢？
推荐资料：
【自制FOC驱动器】深入浅出讲解FOC算法与SVPWM技术 - 知乎
https://www.bilibili.com/video/BV1SS42197Sv(最易懂的SVPWM讲解)
https://www.bilibili.com/video/BV18ftSe9E25
四、电角度零点校准（闭环）
本人从刚开始闭环的时候开始到这里的闭环都深受电角度正负号的困扰。开始写完帕克逆变换和SVPWM之后把编码器转换得到的电角度（机械角度乘极对数）正常输入给帕克逆变换结果发现电机在原地抖，在得到的电角度前加个负号就可以正常转动了。后面在闭环的时候帕克变换正常输入上面已经加好负号的电角度，发现iq、id居然呈现类似两项正弦波的变化规律，在帕克变换的电角度前也加一个负号就可以了。虽然问题已经解决，但是我们最好还是搞清楚为什么我们这样做就可以解决遇到的问题。
首先帕克变换我们知道就是将两项正弦波配合上帕克变换参考系的同步旋转，使得两项正弦波在帕克变换参考系上分解为定值
我们反过来想，那么假如我想让电机顺时针转，CH1、CH2、CH3的变化规律就是已知的，进而可以知道两相正弦波也是已知的。而两相正弦波确定了的话。想要让id、iq为恒定值的话我就必须让帕克变换参考系和dq轴同步转动，想要同步转动，那么帕克变换参考系的旋转速度（机械角度转电角度）和旋转方向（本节重点）就是确定的了。
那么正着来是什么流程呢？首先我给定一个固定的ud、uq以及输入帕克参考系同步转动需要的参数（静态来说就是电角度）此时由帕克逆变换和SVPWM得到的Ta、Tb、Tc就会拖着电机转动，电机转动电角度改变，Ta、Tb、Tc也改变，继续拖着电机转动。这是理想情况，假如方向错了会怎么样呢？电机转动电角度改变，只不过这次由机械角度得到的电角度方向是反的，帕克参考系和电机转动方向就是反的，当iq足够大的时候电机就会发生震荡。
如果把上面的系统看作一个无阻力的箱子，正确的旋转方向就像是你朝左推这个箱子，这个箱子就向左输出一个力，这样这个箱子自然可以被你推着走。方向不对的话就像是你往左推这个箱子，这个箱子反而向右输出一个力，就像是在和你对抗一样，也有点像是有了一个摩擦力无穷大的箱子。我们当然也就不能推动他，反应到电机上就像是被锁在了原地一样
上面我们已经知道了如果电角度方向不对会导致电机锁在原地。那么是什么决定或者说规定了电角度方向呢？答案是数学。数学约定的一致性
FOC变换基于Park变换和Clarke变换，这些变换都遵循标准的数学坐标系约定：
在复平面或二维坐标系中，角度通常定义为从正实轴（或x轴）开始，逆时针方向为正
这确保了三角函数 cosθ 和 sinθ 的符号关系正确
如果你不想了解这些的话你只需要知道电角度由于数学上的约定，一定是逆时针增大的，如果你逆时针旋转电机发现电角度减小，那么就在你的机械角度上加个负号以保持电角度方向的正确。
2025.9.3 电角度可以不用固定顺时针增大，因为我们只要保证电角度方向（由实际电机的电机转动情况决定）和电机转动方向（由你的ABC三相决定）是一致的即可，如果你的电机给uq他像是锁在了原地，那么你就要考虑是不是应该在电角度转机械角度前加个负号。FOC的三相线是不可以随便调换的，调换两项可以改变旋转方向那个是无感六步换向才有的特性。
本人在尝试过很多种零点校准的方法之后最后选择了最简单的电角度给0，给个稍微大一点的ud，让电机锁在一个地方，读取此时机械角度，转化为电角度。该值就是电角度的偏移值，在主循环时减去该值即可。
以下附电角度校准代码
/**
* @brief 电机角度校准
* @param p_angle_offset 输出参数，电机角度偏移
* @return 电机角度偏移
*/
float32_t FOC_Electrical_Angle_Calibration(float32_t* p_angle_offset)
{
float32_t sin_theta, cos_theta;
float32_t Ualpha_Calibration, Ubeta_Calibration;
float32_t Ta_Calibration, Tb_Calibration, Tc_Calibration;
float32_t electrical_offset=0;
RAD_TO_ARM_SIN_COS(0.0f, &sin_theta, &cos_theta);
//帕克逆变换，将两项静止项转换为两项正弦波，并领先于当前位置
Inverse_Park_Transform(1.5f,0,&Ualpha_Calibration,&Ubeta_Calibration,sin_theta,cos_theta);
//计算扇区,通过SVPWM算法生成三相马鞍波
SVPWM_Calculate(Ualpha_Calibration,Ubeta_Calibration,24,__HAL_TIM_GET_AUTORELOAD(&htim1),&Ta_Calibration,&Tb_Calibration,&Tc_Calibration);
//输出计算结果
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_1, Ta_Calibration);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_2, Tb_Calibration);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_3, Tc_Calibration);
osDelay(500);
// 计算电机角度偏移
Mechanical_To_Electrical_Angle(motor_state_data.angle,7,0,1,&electrical_offset);
//关闭所有PWM输出，电机断电
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_1, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_2, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_3, 0);
*p_angle_offset=electrical_offset;
return electrical_offset;
}附电流偏移校准代码
/**
* @brief 电流零点校准
* @param samples 采样次数，建议1000-2000
* @param Ia_offset 返回Ia零点偏移
* @param Ib_offset 返回Ib零点偏移
* @param Ic_offset 返回Ic零点偏移 (可选)
*/
void FOC_Current_Zero_Calibration(const uint16_t samples, float *Ia_offset, float *Ib_offset, float *Ic_offset)
{
float32_t Ia_sum = 0, Ib_sum = 0, Ic_sum = 0;
// 关闭所有PWM输出，确保电机断电
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_1, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_2, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_3, 0);
osDelay(200); // 等待电机完全静止
// 多次采样求平均
for(uint16_t i = 0; i < samples; i++) {
Ia_sum += motor_state_data.Ia_raw;
Ib_sum += motor_state_data.Ib_raw;
if(Ic_offset != NULL) {
Ic_sum += motor_state_data.Ic_raw;
}
osDelay(1);
}
// 计算平均值
*Ia_offset = Ia_sum / (float)samples;
*Ib_offset = Ib_sum / (float)samples;
if(Ic_offset != NULL) {
*Ic_offset = Ic_sum / (float)samples;
}
}再来电机震动发声代码
/**
* @brief 驱动电机播放指定音调
* @details D轴震荡，从而使电机振动发声。
*
* @param frequency 音调的频率 (Hz)。例如，440Hz 就是标准音A。如果为0，则为静音。
* @param duration_ms 音调持续时间 (毫秒)。
* @param voltage 产生音调的电压幅值(V)。这会影响音量。建议值 0.5V - 1.5V。
* 注意：电压过高可能导致电机在发声时轻微转动或过热。
* @param vdc 直流母线电压(V)，用于SVPWM计算。
*/
void Motor_Play_Tone(float frequency, uint16_t duration_ms, float voltage, float vdc,float angle_offset)
{
if (frequency <= 0.0f) {
//静音部分代码
return;
}
// 定位到物理d轴
// 我们只需要在开始时计算一次sin/cos，因为磁场的方向是固定的
float sin_theta = sinf(angle_offset);
float cos_theta = cosf(angle_offset);
// 使用DWT进行高精度计时
uint32_t start_cycles = DWT->CYCCNT; // 直接访问
uint32_t duration_cycles = duration_ms * (SystemCoreClock / 1000);
uint32_t current_cycles = start_cycles;
uint32_t tim_period = __HAL_TIM_GET_AUTORELOAD(&htim1);
while ((current_cycles - start_cycles) < duration_cycles) {
current_cycles = DWT->CYCCNT; // 直接访问
// 创建一个音频频率的正弦波信号
float elapsed_time_s = (float)(current_cycles - start_cycles) / SystemCoreClock;
float sound_wave = sinf(2.0f * PI * frequency * elapsed_time_s);
// 将音频信号注入到d轴，q轴保持为0
float Ud = voltage * sound_wave;
float Uq = 0.0f;
// 使用逆Park变换，将d/q电压转换到定子坐标系
// 注意：这里的sin_theta和cos_theta是固定的，代表d轴方向
float Ualpha, Ubeta;
Inverse_Park_Transform(Ud, Uq, &Ualpha, &Ubeta, sin_theta, cos_theta);
// SVPWM输出
float32_t Ta, Tb, Tc;
SVPWM_Calculate(Ualpha, Ubeta, vdc, tim_period, &Ta, &Tb, &Tc);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_1, (uint32_t)Ta);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_2, (uint32_t)Tb);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_3, (uint32_t)Tc);
}
// 音调结束后，确保电机完全停止
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_1, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_2, 0);
__HAL_TIM_SET_COMPARE(&htim1, TIM_CHANNEL_3, 0);
}P6.电角度校准对齐【STM32软硬件复刻DengFoc例子合集】（此人的合集对电角度与校准问题很深入）
五、实际效果
声音有些嘶哑是因为程序运行过程需要进行调试，所以在循环中加入了数据打印，关闭打印后声音很丝滑
力矩闭环效果
速度闭环效果
位置闭环效果
最终效果
高频注入不了我就注入音乐，嘟~嘟~嘟~
评论区